Command:
$ echo $(date +%Y%m%d%H%M%S) /dir1 http://www.apple.com | self 1.9.2 3.8 2.2
Result:
08 www.apple.com dir1
Sunday, October 2, 2016
Thursday, September 29, 2016
Python: Matplotlib: Mathtext Examples
Noteworthy:
matplotlib.pyplot.fill_between()
Command:
$ cat Downloads/mathtext_examples.py
Result:
"""
Selected features of Matplotlib's math rendering engine.
"""
from __future__ import print_function
import matplotlib.pyplot as plt
import os
import sys
import re
import gc
# Selection of features following "Writing mathematical expressions" tutorial
mathtext_titles = {
0: "Header demo",
1: "Subscripts and superscripts",
2: "Fractions, binomials and stacked numbers",
3: "Radicals",
4: "Fonts",
5: "Accents",
6: "Greek, Hebrew",
7: "Delimiters, functions and Symbols"}
n_lines = len(mathtext_titles)
# Randomly picked examples
mathext_demos = {
0: r"$W^{3\beta}_{\delta_1 \rho_1 \sigma_2} = "
r"U^{3\beta}_{\delta_1 \rho_1} + \frac{1}{8 \pi 2} "
r"\int^{\alpha_2}_{\alpha_2} d \alpha^\prime_2 \left[\frac{ "
r"U^{2\beta}_{\delta_1 \rho_1} - \alpha^\prime_2U^{1\beta}_"
r"{\rho_1 \sigma_2} }{U^{0\beta}_{\rho_1 \sigma_2}}\right]$",
1: r"$\alpha_i > \beta_i,\ "
r"\alpha_{i+1}^j = {\rm sin}(2\pi f_j t_i) e^{-5 t_i/\tau},\ "
r"\ldots$",
2: r"$\frac{3}{4},\ \binom{3}{4},\ \stackrel{3}{4},\ "
r"\left(\frac{5 - \frac{1}{x}}{4}\right),\ \ldots$",
3: r"$\sqrt{2},\ \sqrt[3]{x},\ \ldots$",
4: r"$\mathrm{Roman}\ , \ \mathit{Italic}\ , \ \mathtt{Typewriter} \ "
r"\mathrm{or}\ \mathcal{CALLIGRAPHY}$",
5: r"$\acute a,\ \bar a,\ \breve a,\ \dot a,\ \ddot a, \ \grave a, \ "
r"\hat a,\ \tilde a,\ \vec a,\ \widehat{xyz},\ \widetilde{xyz},\ "
r"\ldots$",
6: r"$\alpha,\ \beta,\ \chi,\ \delta,\ \lambda,\ \mu,\ "
r"\Delta,\ \Gamma,\ \Omega,\ \Phi,\ \Pi,\ \Upsilon,\ \nabla,\ "
r"\aleph,\ \beth,\ \daleth,\ \gimel,\ \ldots$",
7: r"$\coprod,\ \int,\ \oint,\ \prod,\ \sum,\ "
r"\log,\ \sin,\ \approx,\ \oplus,\ \star,\ \varpropto,\ "
r"\infty,\ \partial,\ \Re,\ \leftrightsquigarrow, \ \ldots$"}
def doall():
# Colors used in mpl online documentation.
mpl_blue_rvb = (191./255., 209./256., 212./255.)
mpl_orange_rvb = (202/255., 121/256., 0./255.)
mpl_grey_rvb = (51./255., 51./255., 51./255.)
# Creating figure and axis.
plt.figure(figsize=(6, 7))
plt.axes([0.01, 0.01, 0.98, 0.90], axisbg="white", frameon=True)
plt.gca().set_xlim(0., 1.)
plt.gca().set_ylim(0., 1.)
plt.gca().set_title("Matplotlib's math rendering engine",
color=mpl_grey_rvb, fontsize=14, weight='bold')
plt.gca().set_xticklabels("", visible=False)
plt.gca().set_yticklabels("", visible=False)
# Gap between lines in axes coords
line_axesfrac = (1. / (n_lines))
# Plotting header demonstration formula
full_demo = mathext_demos[0]
plt.annotate(full_demo,
xy=(0.5, 1. - 0.59*line_axesfrac),
xycoords='data', color=mpl_orange_rvb, ha='center',
fontsize=20)
# Plotting features demonstration formulae
for i_line in range(1, n_lines):
baseline = 1. - (i_line)*line_axesfrac
baseline_next = baseline - line_axesfrac*1.
title = mathtext_titles[i_line] + ":"
fill_color = ['white', mpl_blue_rvb][i_line % 2]
plt.fill_between([0., 1.], [baseline, baseline],
[baseline_next, baseline_next],
color=fill_color, alpha=0.5)
plt.annotate(title,
xy=(0.07, baseline - 0.3*line_axesfrac),
xycoords='data', color=mpl_grey_rvb, weight='bold')
demo = mathext_demos[i_line]
plt.annotate(demo,
xy=(0.05, baseline - 0.75*line_axesfrac),
xycoords='data', color=mpl_grey_rvb,
fontsize=16)
for i in range(n_lines):
s = mathext_demos[i]
print(i, s)
plt.savefig('pyplot_mathtext_examples.png')
if '--latex' in sys.argv:
# Run: python mathtext_examples.py --latex
# Need amsmath and amssymb packages.
fd = open("mathtext_examples.ltx", "w")
fd.write("\\documentclass{article}\n")
fd.write("\\usepackage{amsmath, amssymb}\n")
fd.write("\\begin{document}\n")
fd.write("\\begin{enumerate}\n")
for i in range(n_lines):
s = mathext_demos[i]
s = re.sub(r"(?<!\\)\$", "$$", s)
fd.write("\\item %s\n" % s)
fd.write("\\end{enumerate}\n")
fd.write("\\end{document}\n")
fd.close()
os.system("pdflatex mathtext_examples.ltx")
else:
doall()
Command:
$ python Downloads/mathtext_examples.py
Result:
0 $W^{3\beta}_{\delta_1 \rho_1 \sigma_2} = U^{3\beta}_{\delta_1 \rho_1} + \frac{1}{8 \pi 2} \int^{\alpha_2}_{\alpha_2} d \alpha^\prime_2 \left[\frac{ U^{2\beta}_{\delta_1 \rho_1} - \alpha^\prime_2U^{1\beta}_{\rho_1 \sigma_2} }{U^{0\beta}_{\rho_1 \sigma_2}}\right]$
1 $\alpha_i > \beta_i,\ \alpha_{i+1}^j = {\rm sin}(2\pi f_j t_i) e^{-5 t_i/\tau},\ \ldots$
2 $\frac{3}{4},\ \binom{3}{4},\ \stackrel{3}{4},\ \left(\frac{5 - \frac{1}{x}}{4}\right),\ \ldots$
3 $\sqrt{2},\ \sqrt[3]{x},\ \ldots$
4 $\mathrm{Roman}\ , \ \mathit{Italic}\ , \ \mathtt{Typewriter} \ \mathrm{or}\ \mathcal{CALLIGRAPHY}$
5 $\acute a,\ \bar a,\ \breve a,\ \dot a,\ \ddot a, \ \grave a, \ \hat a,\ \tilde a,\ \vec a,\ \widehat{xyz},\ \widetilde{xyz},\ \ldots$
6 $\alpha,\ \beta,\ \chi,\ \delta,\ \lambda,\ \mu,\ \Delta,\ \Gamma,\ \Omega,\ \Phi,\ \Pi,\ \Upsilon,\ \nabla,\ \aleph,\ \beth,\ \daleth,\ \gimel,\ \ldots$
7 $\coprod,\ \int,\ \oint,\ \prod,\ \sum,\ \log,\ \sin,\ \approx,\ \oplus,\ \star,\ \varpropto,\ \infty,\ \partial,\ \Re,\ \leftrightsquigarrow, \ \ldots$
Graphical output:
matplotlib.pyplot.fill_between()
Command:
$ cat Downloads/mathtext_examples.py
Result:
"""
Selected features of Matplotlib's math rendering engine.
"""
from __future__ import print_function
import matplotlib.pyplot as plt
import os
import sys
import re
import gc
# Selection of features following "Writing mathematical expressions" tutorial
mathtext_titles = {
0: "Header demo",
1: "Subscripts and superscripts",
2: "Fractions, binomials and stacked numbers",
3: "Radicals",
4: "Fonts",
5: "Accents",
6: "Greek, Hebrew",
7: "Delimiters, functions and Symbols"}
n_lines = len(mathtext_titles)
# Randomly picked examples
mathext_demos = {
0: r"$W^{3\beta}_{\delta_1 \rho_1 \sigma_2} = "
r"U^{3\beta}_{\delta_1 \rho_1} + \frac{1}{8 \pi 2} "
r"\int^{\alpha_2}_{\alpha_2} d \alpha^\prime_2 \left[\frac{ "
r"U^{2\beta}_{\delta_1 \rho_1} - \alpha^\prime_2U^{1\beta}_"
r"{\rho_1 \sigma_2} }{U^{0\beta}_{\rho_1 \sigma_2}}\right]$",
1: r"$\alpha_i > \beta_i,\ "
r"\alpha_{i+1}^j = {\rm sin}(2\pi f_j t_i) e^{-5 t_i/\tau},\ "
r"\ldots$",
2: r"$\frac{3}{4},\ \binom{3}{4},\ \stackrel{3}{4},\ "
r"\left(\frac{5 - \frac{1}{x}}{4}\right),\ \ldots$",
3: r"$\sqrt{2},\ \sqrt[3]{x},\ \ldots$",
4: r"$\mathrm{Roman}\ , \ \mathit{Italic}\ , \ \mathtt{Typewriter} \ "
r"\mathrm{or}\ \mathcal{CALLIGRAPHY}$",
5: r"$\acute a,\ \bar a,\ \breve a,\ \dot a,\ \ddot a, \ \grave a, \ "
r"\hat a,\ \tilde a,\ \vec a,\ \widehat{xyz},\ \widetilde{xyz},\ "
r"\ldots$",
6: r"$\alpha,\ \beta,\ \chi,\ \delta,\ \lambda,\ \mu,\ "
r"\Delta,\ \Gamma,\ \Omega,\ \Phi,\ \Pi,\ \Upsilon,\ \nabla,\ "
r"\aleph,\ \beth,\ \daleth,\ \gimel,\ \ldots$",
7: r"$\coprod,\ \int,\ \oint,\ \prod,\ \sum,\ "
r"\log,\ \sin,\ \approx,\ \oplus,\ \star,\ \varpropto,\ "
r"\infty,\ \partial,\ \Re,\ \leftrightsquigarrow, \ \ldots$"}
def doall():
# Colors used in mpl online documentation.
mpl_blue_rvb = (191./255., 209./256., 212./255.)
mpl_orange_rvb = (202/255., 121/256., 0./255.)
mpl_grey_rvb = (51./255., 51./255., 51./255.)
# Creating figure and axis.
plt.figure(figsize=(6, 7))
plt.axes([0.01, 0.01, 0.98, 0.90], axisbg="white", frameon=True)
plt.gca().set_xlim(0., 1.)
plt.gca().set_ylim(0., 1.)
plt.gca().set_title("Matplotlib's math rendering engine",
color=mpl_grey_rvb, fontsize=14, weight='bold')
plt.gca().set_xticklabels("", visible=False)
plt.gca().set_yticklabels("", visible=False)
# Gap between lines in axes coords
line_axesfrac = (1. / (n_lines))
# Plotting header demonstration formula
full_demo = mathext_demos[0]
plt.annotate(full_demo,
xy=(0.5, 1. - 0.59*line_axesfrac),
xycoords='data', color=mpl_orange_rvb, ha='center',
fontsize=20)
# Plotting features demonstration formulae
for i_line in range(1, n_lines):
baseline = 1. - (i_line)*line_axesfrac
baseline_next = baseline - line_axesfrac*1.
title = mathtext_titles[i_line] + ":"
fill_color = ['white', mpl_blue_rvb][i_line % 2]
plt.fill_between([0., 1.], [baseline, baseline],
[baseline_next, baseline_next],
color=fill_color, alpha=0.5)
plt.annotate(title,
xy=(0.07, baseline - 0.3*line_axesfrac),
xycoords='data', color=mpl_grey_rvb, weight='bold')
demo = mathext_demos[i_line]
plt.annotate(demo,
xy=(0.05, baseline - 0.75*line_axesfrac),
xycoords='data', color=mpl_grey_rvb,
fontsize=16)
for i in range(n_lines):
s = mathext_demos[i]
print(i, s)
plt.savefig('pyplot_mathtext_examples.png')
if '--latex' in sys.argv:
# Run: python mathtext_examples.py --latex
# Need amsmath and amssymb packages.
fd = open("mathtext_examples.ltx", "w")
fd.write("\\documentclass{article}\n")
fd.write("\\usepackage{amsmath, amssymb}\n")
fd.write("\\begin{document}\n")
fd.write("\\begin{enumerate}\n")
for i in range(n_lines):
s = mathext_demos[i]
s = re.sub(r"(?<!\\)\$", "$$", s)
fd.write("\\item %s\n" % s)
fd.write("\\end{enumerate}\n")
fd.write("\\end{document}\n")
fd.close()
os.system("pdflatex mathtext_examples.ltx")
else:
doall()
Command:
$ python Downloads/mathtext_examples.py
Result:
0 $W^{3\beta}_{\delta_1 \rho_1 \sigma_2} = U^{3\beta}_{\delta_1 \rho_1} + \frac{1}{8 \pi 2} \int^{\alpha_2}_{\alpha_2} d \alpha^\prime_2 \left[\frac{ U^{2\beta}_{\delta_1 \rho_1} - \alpha^\prime_2U^{1\beta}_{\rho_1 \sigma_2} }{U^{0\beta}_{\rho_1 \sigma_2}}\right]$
1 $\alpha_i > \beta_i,\ \alpha_{i+1}^j = {\rm sin}(2\pi f_j t_i) e^{-5 t_i/\tau},\ \ldots$
2 $\frac{3}{4},\ \binom{3}{4},\ \stackrel{3}{4},\ \left(\frac{5 - \frac{1}{x}}{4}\right),\ \ldots$
3 $\sqrt{2},\ \sqrt[3]{x},\ \ldots$
4 $\mathrm{Roman}\ , \ \mathit{Italic}\ , \ \mathtt{Typewriter} \ \mathrm{or}\ \mathcal{CALLIGRAPHY}$
5 $\acute a,\ \bar a,\ \breve a,\ \dot a,\ \ddot a, \ \grave a, \ \hat a,\ \tilde a,\ \vec a,\ \widehat{xyz},\ \widetilde{xyz},\ \ldots$
6 $\alpha,\ \beta,\ \chi,\ \delta,\ \lambda,\ \mu,\ \Delta,\ \Gamma,\ \Omega,\ \Phi,\ \Pi,\ \Upsilon,\ \nabla,\ \aleph,\ \beth,\ \daleth,\ \gimel,\ \ldots$
7 $\coprod,\ \int,\ \oint,\ \prod,\ \sum,\ \log,\ \sin,\ \approx,\ \oplus,\ \star,\ \varpropto,\ \infty,\ \partial,\ \Re,\ \leftrightsquigarrow, \ \ldots$
Graphical output:
 |
| pyplot_mathtext_examples.png |
Python: Matplotlib: XKCD-Style Sketch Plot Example
Noteworthy:
matplotlib.pyplot.xkcd()
matplotlib.pyplot.annotate()
Command:
$ cat Downloads/xkcd.py
Result:
import matplotlib.pyplot as plt
import numpy as np
with plt.xkcd():
# Based on "Stove Ownership" from XKCD by Randall Monroe
# http://xkcd.com/418/
fig = plt.figure()
ax = fig.add_axes((0.1, 0.2, 0.8, 0.7))
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
plt.xticks([])
plt.yticks([])
ax.set_ylim([-30, 10])
data = np.ones(100)
data[70:] -= np.arange(30)
plt.annotate(
'THE DAY I REALIZED\nI COULD COOK BACON\nWHENEVER I WANTED',
xy=(70, 1), arrowprops=dict(arrowstyle='->'), xytext=(15, -10))
plt.plot(data)
plt.xlabel('time')
plt.ylabel('my overall health')
fig.text(
0.5, 0.05,
'"Stove Ownership" from xkcd by Randall Monroe',
ha='center')
plt.savefig('pyplot_xkcd_figure1.png')
# Based on "The Data So Far" from XKCD by Randall Monroe
# http://xkcd.com/373/
fig = plt.figure()
ax = fig.add_axes((0.1, 0.2, 0.8, 0.7))
ax.bar([-0.125, 1.0 - 0.125], [0, 100], 0.25)
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.set_xticks([0, 1])
ax.set_xlim([-0.5, 1.5])
ax.set_ylim([0, 110])
ax.set_xticklabels(['CONFIRMED BY\nEXPERIMENT', 'REFUTED BY\nEXPERIMENT'])
plt.yticks([])
plt.title("CLAIMS OF SUPERNATURAL POWERS")
fig.text(
0.5, 0.05,
'"The Data So Far" from xkcd by Randall Monroe',
ha='center')
plt.savefig('pyplot_xkcd_figure2.png')
plt.show()
matplotlib.pyplot.xkcd()
matplotlib.pyplot.annotate()
Command:
$ cat Downloads/xkcd.py
Result:
import matplotlib.pyplot as plt
import numpy as np
with plt.xkcd():
# Based on "Stove Ownership" from XKCD by Randall Monroe
# http://xkcd.com/418/
fig = plt.figure()
ax = fig.add_axes((0.1, 0.2, 0.8, 0.7))
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
plt.xticks([])
plt.yticks([])
ax.set_ylim([-30, 10])
data = np.ones(100)
data[70:] -= np.arange(30)
plt.annotate(
'THE DAY I REALIZED\nI COULD COOK BACON\nWHENEVER I WANTED',
xy=(70, 1), arrowprops=dict(arrowstyle='->'), xytext=(15, -10))
plt.plot(data)
plt.xlabel('time')
plt.ylabel('my overall health')
fig.text(
0.5, 0.05,
'"Stove Ownership" from xkcd by Randall Monroe',
ha='center')
plt.savefig('pyplot_xkcd_figure1.png')
# Based on "The Data So Far" from XKCD by Randall Monroe
# http://xkcd.com/373/
fig = plt.figure()
ax = fig.add_axes((0.1, 0.2, 0.8, 0.7))
ax.bar([-0.125, 1.0 - 0.125], [0, 100], 0.25)
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.set_xticks([0, 1])
ax.set_xlim([-0.5, 1.5])
ax.set_ylim([0, 110])
ax.set_xticklabels(['CONFIRMED BY\nEXPERIMENT', 'REFUTED BY\nEXPERIMENT'])
plt.yticks([])
plt.title("CLAIMS OF SUPERNATURAL POWERS")
fig.text(
0.5, 0.05,
'"The Data So Far" from xkcd by Randall Monroe',
ha='center')
plt.savefig('pyplot_xkcd_figure2.png')
plt.show()
Graphical output:
 |
| pyplot_xkcd_figure1.png |
 |
| pyplot_xkcd_figure2.png |
Python: Matplotlib: Polar Plot Example
Noteworthy:
ax.set_rmax()
Command:
$ cat Downloads/polar_demo.py
Result:
"""
Demo of a line plot on a polar axis.
"""
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('dark_background')
r = np.arange(0, 3.0, 0.01)
theta = 2 * np.pi * r
ax = plt.subplot(111, projection='polar')
ax.plot(theta, r, color='r', linewidth=3)
ax.set_rmax(2.0)
ax.grid(True)
ax.set_title("A line plot on a polar axis", va='bottom')
plt.savefig('pyplot_polar_demo.png')
Graphical output:
ax.set_rmax()
Command:
$ cat Downloads/polar_demo.py
Result:
"""
Demo of a line plot on a polar axis.
"""
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('dark_background')
r = np.arange(0, 3.0, 0.01)
theta = 2 * np.pi * r
ax = plt.subplot(111, projection='polar')
ax.plot(theta, r, color='r', linewidth=3)
ax.set_rmax(2.0)
ax.grid(True)
ax.set_title("A line plot on a polar axis", va='bottom')
plt.savefig('pyplot_polar_demo.png')
Graphical output:
 |
| pyplot_polar_demo.png |
Python: Matplotlib: Logarithm Example
Noteworthy:
matplotlib.pyplot.subplots_adjust()
numpy.arange()
matplotlib.pyplot.semilogy()
matplotlib.pyplot.semilogx()
matplotlib.pyplot.loglog()
matplotlib.pyplot.errorbar()
Command:
$ cat Downloads/log_demo.py
Result:
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('dark_background')
plt.subplots_adjust(hspace=0.4)
t = np.arange(0.01, 20.0, 0.01)
# log y axis
plt.subplot(221)
plt.semilogy(t, np.exp(-t/5.0))
plt.title('semilogy')
plt.grid(True)
# log x axis
plt.subplot(222)
plt.semilogx(t, np.sin(2*np.pi*t))
plt.title('semilogx')
plt.grid(True)
# log x and y axis
plt.subplot(223)
plt.loglog(t, 20*np.exp(-t/10.0), basex=2)
plt.grid(True)
plt.title('loglog base 4 on x')
# with errorbars: clip non-positive values
ax = plt.subplot(224)
ax.set_xscale("log", nonposx='clip')
ax.set_yscale("log", nonposy='clip')
x = 10.0**np.linspace(0.0, 2.0, 20)
y = x**2.0
plt.errorbar(x, y, xerr=0.1*x, yerr=5.0 + 0.75*y)
ax.set_ylim(ymin=0.1)
ax.set_title('Errorbars go negative')
plt.savefig('pyplot_log_demo.png')
Command:
$ python Downloads/log_demo.py
Graphical output:
matplotlib.pyplot.subplots_adjust()
numpy.arange()
matplotlib.pyplot.semilogy()
matplotlib.pyplot.semilogx()
matplotlib.pyplot.loglog()
matplotlib.pyplot.errorbar()
Command:
$ cat Downloads/log_demo.py
Result:
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('dark_background')
plt.subplots_adjust(hspace=0.4)
t = np.arange(0.01, 20.0, 0.01)
# log y axis
plt.subplot(221)
plt.semilogy(t, np.exp(-t/5.0))
plt.title('semilogy')
plt.grid(True)
# log x axis
plt.subplot(222)
plt.semilogx(t, np.sin(2*np.pi*t))
plt.title('semilogx')
plt.grid(True)
# log x and y axis
plt.subplot(223)
plt.loglog(t, 20*np.exp(-t/10.0), basex=2)
plt.grid(True)
plt.title('loglog base 4 on x')
# with errorbars: clip non-positive values
ax = plt.subplot(224)
ax.set_xscale("log", nonposx='clip')
ax.set_yscale("log", nonposy='clip')
x = 10.0**np.linspace(0.0, 2.0, 20)
y = x**2.0
plt.errorbar(x, y, xerr=0.1*x, yerr=5.0 + 0.75*y)
ax.set_ylim(ymin=0.1)
ax.set_title('Errorbars go negative')
plt.savefig('pyplot_log_demo.png')
Command:
$ python Downloads/log_demo.py
Graphical output:
 |
| pyplot_log_demo..png |
Python: Matplotlib: Finance Example
Noteworthy:
datetime.date(2006, 1, 1)
datetime.date.today()
finance.fetch_historical_yahoo(ticker, startdate, enddate)
mlab.csv2rec(fh)
fh.close()
r.sort()
np.asarray(x)
np.ones(n)
weights.sum()
np.convolve(x, weights, mode='full')[:len(x)]
np.diff(prices)
np.zeros_like(prices)
...
Command:
$ cat Downloads/finance_work2.py
Result:
import datetime
import numpy as np
import matplotlib.colors as colors
import matplotlib.finance as finance
import matplotlib.dates as mdates
import matplotlib.ticker as mticker
import matplotlib.mlab as mlab
import matplotlib.pyplot as plt
import matplotlib.font_manager as font_manager
plt.style.use('dark_background')
startdate = datetime.date(2006, 1, 1)
today = enddate = datetime.date.today()
ticker = 'SPY'
fh = finance.fetch_historical_yahoo(ticker, startdate, enddate)
# a numpy record array with fields: date, open, high, low, close, volume, adj_close)
r = mlab.csv2rec(fh)
fh.close()
r.sort()
def moving_average(x, n, type='simple'):
"""
compute an n period moving average.
type is 'simple' | 'exponential'
"""
x = np.asarray(x)
if type == 'simple':
weights = np.ones(n)
else:
weights = np.exp(np.linspace(-1., 0., n))
weights /= weights.sum()
a = np.convolve(x, weights, mode='full')[:len(x)]
a[:n] = a[n]
return a
def relative_strength(prices, n=14):
"""
compute the n period relative strength indicator
http://stockcharts.com/school/doku.php?id=chart_school:glossary_r#relativestrengthindex
http://www.investopedia.com/terms/r/rsi.asp
"""
deltas = np.diff(prices)
seed = deltas[:n+1]
up = seed[seed >= 0].sum()/n
down = -seed[seed < 0].sum()/n
rs = up/down
rsi = np.zeros_like(prices)
rsi[:n] = 100. - 100./(1. + rs)
for i in range(n, len(prices)):
delta = deltas[i - 1] # cause the diff is 1 shorter
if delta > 0:
upval = delta
downval = 0.
else:
upval = 0.
downval = -delta
up = (up*(n - 1) + upval)/n
down = (down*(n - 1) + downval)/n
rs = up/down
rsi[i] = 100. - 100./(1. + rs)
return rsi
def moving_average_convergence(x, nslow=26, nfast=12):
"""
compute the MACD (Moving Average Convergence/Divergence) using a fast and slow exponential moving avg'
return value is emaslow, emafast, macd which are len(x) arrays
"""
emaslow = moving_average(x, nslow, type='exponential')
emafast = moving_average(x, nfast, type='exponential')
return emaslow, emafast, emafast - emaslow
plt.rc('axes', grid=True)
plt.rc('grid', color='0.75', linestyle='-', linewidth=0.5)
textsize = 9
left, width = 0.1, 0.8
rect1 = [left, 0.7, width, 0.2]
rect2 = [left, 0.3, width, 0.4]
rect3 = [left, 0.1, width, 0.2]
fig = plt.figure(facecolor='white')
axescolor = '#f6f6f6' # the axes background color
ax1 = fig.add_axes(rect1, axisbg=axescolor) # left, bottom, width, height
ax2 = fig.add_axes(rect2, axisbg=axescolor, sharex=ax1)
ax2t = ax2.twinx()
ax3 = fig.add_axes(rect3, axisbg=axescolor, sharex=ax1)
# plot the relative strength indicator
prices = r.adj_close
rsi = relative_strength(prices)
fillcolor = 'darkgoldenrod'
ax1.plot(r.date, rsi, color=fillcolor)
ax1.axhline(70, color=fillcolor)
ax1.axhline(30, color=fillcolor)
ax1.fill_between(r.date, rsi, 70, where=(rsi >= 70), facecolor=fillcolor, edgecolor=fillcolor)
ax1.fill_between(r.date, rsi, 30, where=(rsi <= 30), facecolor=fillcolor, edgecolor=fillcolor)
ax1.text(0.6, 0.9, '>70 = overbought', va='top', transform=ax1.transAxes, fontsize=textsize)
ax1.text(0.6, 0.1, '<30 = oversold', transform=ax1.transAxes, fontsize=textsize)
ax1.set_ylim(0, 100)
ax1.set_yticks([30, 70])
ax1.text(0.025, 0.95, 'RSI (14)', va='top', transform=ax1.transAxes, fontsize=textsize)
ax1.set_title('%s daily' % ticker)
# plot the price and volume data
dx = r.adj_close - r.close
low = r.low + dx
high = r.high + dx
deltas = np.zeros_like(prices)
deltas[1:] = np.diff(prices)
up = deltas > 0
ax2.vlines(r.date[up], low[up], high[up], color='black', label='_nolegend_')
ax2.vlines(r.date[~up], low[~up], high[~up], color='black', label='_nolegend_')
ma20 = moving_average(prices, 20, type='simple')
ma200 = moving_average(prices, 200, type='simple')
linema20, = ax2.plot(r.date, ma20, color='blue', lw=2, label='MA (20)')
linema200, = ax2.plot(r.date, ma200, color='red', lw=2, label='MA (200)')
last = r[-1]
s = '%s O:%1.2f H:%1.2f L:%1.2f C:%1.2f, V:%1.1fM Chg:%+1.2f' % (
today.strftime('%d-%b-%Y'),
last.open, last.high,
last.low, last.close,
last.volume*1e-6,
last.close - last.open)
t4 = ax2.text(0.3, 0.9, s, transform=ax2.transAxes, fontsize=textsize)
props = font_manager.FontProperties(size=10)
leg = ax2.legend(loc='center left', shadow=True, fancybox=True, prop=props)
leg.get_frame().set_alpha(0.5)
volume = (r.close*r.volume)/1e6 # dollar volume in millions
vmax = volume.max()
poly = ax2t.fill_between(r.date, volume, 0, label='Volume', facecolor=fillcolor, edgecolor=fillcolor)
ax2t.set_ylim(0, 5*vmax)
ax2t.set_yticks([])
# compute the MACD indicator
fillcolor = 'darkslategrey'
nslow = 26
nfast = 12
nema = 9
emaslow, emafast, macd = moving_average_convergence(prices, nslow=nslow, nfast=nfast)
ema9 = moving_average(macd, nema, type='exponential')
ax3.plot(r.date, macd, color='black', lw=2)
ax3.plot(r.date, ema9, color='blue', lw=1)
ax3.fill_between(r.date, macd - ema9, 0, alpha=0.5, facecolor=fillcolor, edgecolor=fillcolor)
ax3.text(0.025, 0.95, 'MACD (%d, %d, %d)' % (nfast, nslow, nema), va='top',
transform=ax3.transAxes, fontsize=textsize)
#ax3.set_yticks([])
# turn off upper axis tick labels, rotate the lower ones, etc
for ax in ax1, ax2, ax2t, ax3:
if ax != ax3:
for label in ax.get_xticklabels():
label.set_visible(False)
else:
for label in ax.get_xticklabels():
label.set_rotation(30)
label.set_horizontalalignment('right')
ax.fmt_xdata = mdates.DateFormatter('%Y-%m-%d')
class MyLocator(mticker.MaxNLocator):
def __init__(self, *args, **kwargs):
mticker.MaxNLocator.__init__(self, *args, **kwargs)
def __call__(self, *args, **kwargs):
return mticker.MaxNLocator.__call__(self, *args, **kwargs)
# at most 5 ticks, pruning the upper and lower so they don't overlap
# with other ticks
#ax2.yaxis.set_major_locator(mticker.MaxNLocator(5, prune='both'))
#ax3.yaxis.set_major_locator(mticker.MaxNLocator(5, prune='both'))
ax2.yaxis.set_major_locator(MyLocator(5, prune='both'))
ax3.yaxis.set_major_locator(MyLocator(5, prune='both'))
plt.savefig("pyplot_finance_work2.png")
Graphical output:
datetime.date(2006, 1, 1)
datetime.date.today()
finance.fetch_historical_yahoo(ticker, startdate, enddate)
mlab.csv2rec(fh)
fh.close()
r.sort()
np.asarray(x)
np.ones(n)
weights.sum()
np.convolve(x, weights, mode='full')[:len(x)]
np.diff(prices)
np.zeros_like(prices)
...
Command:
$ cat Downloads/finance_work2.py
Result:
import datetime
import numpy as np
import matplotlib.colors as colors
import matplotlib.finance as finance
import matplotlib.dates as mdates
import matplotlib.ticker as mticker
import matplotlib.mlab as mlab
import matplotlib.pyplot as plt
import matplotlib.font_manager as font_manager
plt.style.use('dark_background')
startdate = datetime.date(2006, 1, 1)
today = enddate = datetime.date.today()
ticker = 'SPY'
fh = finance.fetch_historical_yahoo(ticker, startdate, enddate)
# a numpy record array with fields: date, open, high, low, close, volume, adj_close)
r = mlab.csv2rec(fh)
fh.close()
r.sort()
def moving_average(x, n, type='simple'):
"""
compute an n period moving average.
type is 'simple' | 'exponential'
"""
x = np.asarray(x)
if type == 'simple':
weights = np.ones(n)
else:
weights = np.exp(np.linspace(-1., 0., n))
weights /= weights.sum()
a = np.convolve(x, weights, mode='full')[:len(x)]
a[:n] = a[n]
return a
def relative_strength(prices, n=14):
"""
compute the n period relative strength indicator
http://stockcharts.com/school/doku.php?id=chart_school:glossary_r#relativestrengthindex
http://www.investopedia.com/terms/r/rsi.asp
"""
deltas = np.diff(prices)
seed = deltas[:n+1]
up = seed[seed >= 0].sum()/n
down = -seed[seed < 0].sum()/n
rs = up/down
rsi = np.zeros_like(prices)
rsi[:n] = 100. - 100./(1. + rs)
for i in range(n, len(prices)):
delta = deltas[i - 1] # cause the diff is 1 shorter
if delta > 0:
upval = delta
downval = 0.
else:
upval = 0.
downval = -delta
up = (up*(n - 1) + upval)/n
down = (down*(n - 1) + downval)/n
rs = up/down
rsi[i] = 100. - 100./(1. + rs)
return rsi
def moving_average_convergence(x, nslow=26, nfast=12):
"""
compute the MACD (Moving Average Convergence/Divergence) using a fast and slow exponential moving avg'
return value is emaslow, emafast, macd which are len(x) arrays
"""
emaslow = moving_average(x, nslow, type='exponential')
emafast = moving_average(x, nfast, type='exponential')
return emaslow, emafast, emafast - emaslow
plt.rc('axes', grid=True)
plt.rc('grid', color='0.75', linestyle='-', linewidth=0.5)
textsize = 9
left, width = 0.1, 0.8
rect1 = [left, 0.7, width, 0.2]
rect2 = [left, 0.3, width, 0.4]
rect3 = [left, 0.1, width, 0.2]
fig = plt.figure(facecolor='white')
axescolor = '#f6f6f6' # the axes background color
ax1 = fig.add_axes(rect1, axisbg=axescolor) # left, bottom, width, height
ax2 = fig.add_axes(rect2, axisbg=axescolor, sharex=ax1)
ax2t = ax2.twinx()
ax3 = fig.add_axes(rect3, axisbg=axescolor, sharex=ax1)
# plot the relative strength indicator
prices = r.adj_close
rsi = relative_strength(prices)
fillcolor = 'darkgoldenrod'
ax1.plot(r.date, rsi, color=fillcolor)
ax1.axhline(70, color=fillcolor)
ax1.axhline(30, color=fillcolor)
ax1.fill_between(r.date, rsi, 70, where=(rsi >= 70), facecolor=fillcolor, edgecolor=fillcolor)
ax1.fill_between(r.date, rsi, 30, where=(rsi <= 30), facecolor=fillcolor, edgecolor=fillcolor)
ax1.text(0.6, 0.9, '>70 = overbought', va='top', transform=ax1.transAxes, fontsize=textsize)
ax1.text(0.6, 0.1, '<30 = oversold', transform=ax1.transAxes, fontsize=textsize)
ax1.set_ylim(0, 100)
ax1.set_yticks([30, 70])
ax1.text(0.025, 0.95, 'RSI (14)', va='top', transform=ax1.transAxes, fontsize=textsize)
ax1.set_title('%s daily' % ticker)
# plot the price and volume data
dx = r.adj_close - r.close
low = r.low + dx
high = r.high + dx
deltas = np.zeros_like(prices)
deltas[1:] = np.diff(prices)
up = deltas > 0
ax2.vlines(r.date[up], low[up], high[up], color='black', label='_nolegend_')
ax2.vlines(r.date[~up], low[~up], high[~up], color='black', label='_nolegend_')
ma20 = moving_average(prices, 20, type='simple')
ma200 = moving_average(prices, 200, type='simple')
linema20, = ax2.plot(r.date, ma20, color='blue', lw=2, label='MA (20)')
linema200, = ax2.plot(r.date, ma200, color='red', lw=2, label='MA (200)')
last = r[-1]
s = '%s O:%1.2f H:%1.2f L:%1.2f C:%1.2f, V:%1.1fM Chg:%+1.2f' % (
today.strftime('%d-%b-%Y'),
last.open, last.high,
last.low, last.close,
last.volume*1e-6,
last.close - last.open)
t4 = ax2.text(0.3, 0.9, s, transform=ax2.transAxes, fontsize=textsize)
props = font_manager.FontProperties(size=10)
leg = ax2.legend(loc='center left', shadow=True, fancybox=True, prop=props)
leg.get_frame().set_alpha(0.5)
volume = (r.close*r.volume)/1e6 # dollar volume in millions
vmax = volume.max()
poly = ax2t.fill_between(r.date, volume, 0, label='Volume', facecolor=fillcolor, edgecolor=fillcolor)
ax2t.set_ylim(0, 5*vmax)
ax2t.set_yticks([])
# compute the MACD indicator
fillcolor = 'darkslategrey'
nslow = 26
nfast = 12
nema = 9
emaslow, emafast, macd = moving_average_convergence(prices, nslow=nslow, nfast=nfast)
ema9 = moving_average(macd, nema, type='exponential')
ax3.plot(r.date, macd, color='black', lw=2)
ax3.plot(r.date, ema9, color='blue', lw=1)
ax3.fill_between(r.date, macd - ema9, 0, alpha=0.5, facecolor=fillcolor, edgecolor=fillcolor)
ax3.text(0.025, 0.95, 'MACD (%d, %d, %d)' % (nfast, nslow, nema), va='top',
transform=ax3.transAxes, fontsize=textsize)
#ax3.set_yticks([])
# turn off upper axis tick labels, rotate the lower ones, etc
for ax in ax1, ax2, ax2t, ax3:
if ax != ax3:
for label in ax.get_xticklabels():
label.set_visible(False)
else:
for label in ax.get_xticklabels():
label.set_rotation(30)
label.set_horizontalalignment('right')
ax.fmt_xdata = mdates.DateFormatter('%Y-%m-%d')
class MyLocator(mticker.MaxNLocator):
def __init__(self, *args, **kwargs):
mticker.MaxNLocator.__init__(self, *args, **kwargs)
def __call__(self, *args, **kwargs):
return mticker.MaxNLocator.__call__(self, *args, **kwargs)
# at most 5 ticks, pruning the upper and lower so they don't overlap
# with other ticks
#ax2.yaxis.set_major_locator(mticker.MaxNLocator(5, prune='both'))
#ax3.yaxis.set_major_locator(mticker.MaxNLocator(5, prune='both'))
ax2.yaxis.set_major_locator(MyLocator(5, prune='both'))
ax3.yaxis.set_major_locator(MyLocator(5, prune='both'))
plt.savefig("pyplot_finance_work2.png")
Graphical output:
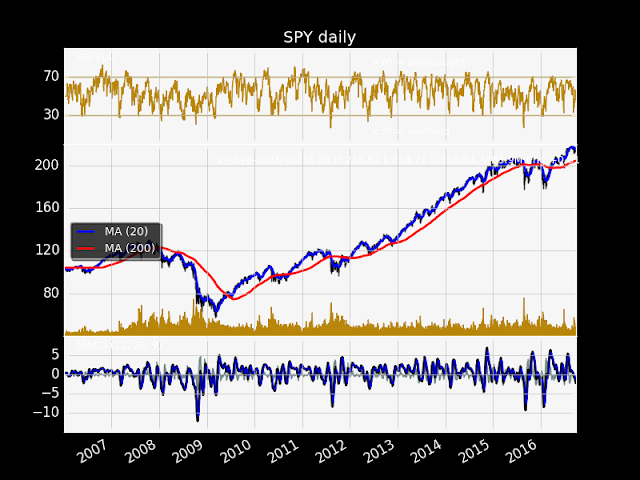 |
| pyplot_finance_work2.png |
Python: Matplotlib: Fill Example
Noteworthy:
matplotlib.pyplot.fill()
Command:
$ cat Downloads/fill_demo.py
Result:
"""
Simple demo of the fill function.
"""
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('dark_background')
x = np.linspace(0, 1)
y = np.sin(4 * np.pi * x) * np.exp(-5 * x)
plt.fill(x, y, 'r')
plt.grid(True)
plt.savefig("pyplot_fill.png")
Graphical output:

matplotlib.pyplot.fill()
Command:
$ cat Downloads/fill_demo.py
Result:
"""
Simple demo of the fill function.
"""
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('dark_background')
x = np.linspace(0, 1)
y = np.sin(4 * np.pi * x) * np.exp(-5 * x)
plt.fill(x, y, 'r')
plt.grid(True)
plt.savefig("pyplot_fill.png")
Command:
$ python Downloads/fill_demo.py
$ open pyplot_fill.png
Graphical output:

Python: Matplotlib: Pie Chart Example
Noteworthy:
matplotlib.pyplot.pie()
ax.pie()
ax.set_xticks()
ax.set_yticks()
ax.set_xticklabels()
ax.set_yticklabels()
ax.set_xlim()
ax.set_ylim()
ax.set_aspect()
Command:
$ cat Downloads/pie_demo_features.py
Result:
"""
Demo of a basic pie chart plus a few additional features.
In addition to the basic pie chart, this demo shows a few optional features:
* slice labels
* auto-labeling the percentage
* offsetting a slice with "explode"
* drop-shadow
* custom start angle
Note about the custom start angle:
The default ``startangle`` is 0, which would start the "Frogs" slice on the
positive x-axis. This example sets ``startangle = 90`` such that everything is
rotated counter-clockwise by 90 degrees, and the frog slice starts on the
positive y-axis.
"""
import matplotlib.pyplot as plt
plt.style.use('dark_background')
# The slices will be ordered and plotted counter-clockwise.
labels = 'Frogs', 'Hogs', 'Dogs', 'Logs'
sizes = [15, 30, 45, 10]
colors = ['yellowgreen', 'gold', 'lightskyblue', 'lightcoral']
explode = (0, 0.1, 0, 0) # only "explode" the 2nd slice (i.e. 'Hogs')
plt.pie(sizes, explode=explode, labels=labels, colors=colors,
autopct='%1.1f%%', shadow=True, startangle=90)
# Set aspect ratio to be equal so that pie is drawn as a circle.
plt.axis('equal')
fig = plt.figure()
ax = fig.gca()
import numpy as np
ax.pie(np.random.random(4), explode=explode, labels=labels, colors=colors,
autopct='%1.1f%%', shadow=True, startangle=90,
radius=0.25, center=(0, 0), frame=True)
ax.pie(np.random.random(4), explode=explode, labels=labels, colors=colors,
autopct='%1.1f%%', shadow=True, startangle=90,
radius=0.25, center=(1, 1), frame=True)
ax.pie(np.random.random(4), explode=explode, labels=labels, colors=colors,
autopct='%1.1f%%', shadow=True, startangle=90,
radius=0.25, center=(0, 1), frame=True)
ax.pie(np.random.random(4), explode=explode, labels=labels, colors=colors,
autopct='%1.1f%%', shadow=True, startangle=90,
radius=0.25, center=(1, 0), frame=True)
ax.set_xticks([0, 1])
ax.set_yticks([0, 1])
ax.set_xticklabels(["Sunny", "Cloudy"])
ax.set_yticklabels(["Dry", "Rainy"])
ax.set_xlim((-0.5, 1.5))
ax.set_ylim((-0.5, 1.5))
# Set aspect ratio to be equal so that pie is drawn as a circle.
ax.set_aspect('equal')
plt.show()
Command:
$ python Downloads/pie_demo_features.py
Graphical output:
matplotlib.pyplot.pie()
ax.pie()
ax.set_xticks()
ax.set_yticks()
ax.set_xticklabels()
ax.set_yticklabels()
ax.set_xlim()
ax.set_ylim()
ax.set_aspect()
Command:
$ cat Downloads/pie_demo_features.py
Result:
"""
Demo of a basic pie chart plus a few additional features.
In addition to the basic pie chart, this demo shows a few optional features:
* slice labels
* auto-labeling the percentage
* offsetting a slice with "explode"
* drop-shadow
* custom start angle
Note about the custom start angle:
The default ``startangle`` is 0, which would start the "Frogs" slice on the
positive x-axis. This example sets ``startangle = 90`` such that everything is
rotated counter-clockwise by 90 degrees, and the frog slice starts on the
positive y-axis.
"""
import matplotlib.pyplot as plt
plt.style.use('dark_background')
# The slices will be ordered and plotted counter-clockwise.
labels = 'Frogs', 'Hogs', 'Dogs', 'Logs'
sizes = [15, 30, 45, 10]
colors = ['yellowgreen', 'gold', 'lightskyblue', 'lightcoral']
explode = (0, 0.1, 0, 0) # only "explode" the 2nd slice (i.e. 'Hogs')
plt.pie(sizes, explode=explode, labels=labels, colors=colors,
autopct='%1.1f%%', shadow=True, startangle=90)
# Set aspect ratio to be equal so that pie is drawn as a circle.
plt.axis('equal')
fig = plt.figure()
ax = fig.gca()
import numpy as np
ax.pie(np.random.random(4), explode=explode, labels=labels, colors=colors,
autopct='%1.1f%%', shadow=True, startangle=90,
radius=0.25, center=(0, 0), frame=True)
ax.pie(np.random.random(4), explode=explode, labels=labels, colors=colors,
autopct='%1.1f%%', shadow=True, startangle=90,
radius=0.25, center=(1, 1), frame=True)
ax.pie(np.random.random(4), explode=explode, labels=labels, colors=colors,
autopct='%1.1f%%', shadow=True, startangle=90,
radius=0.25, center=(0, 1), frame=True)
ax.pie(np.random.random(4), explode=explode, labels=labels, colors=colors,
autopct='%1.1f%%', shadow=True, startangle=90,
radius=0.25, center=(1, 0), frame=True)
ax.set_xticks([0, 1])
ax.set_yticks([0, 1])
ax.set_xticklabels(["Sunny", "Cloudy"])
ax.set_yticklabels(["Dry", "Rainy"])
ax.set_xlim((-0.5, 1.5))
ax.set_ylim((-0.5, 1.5))
# Set aspect ratio to be equal so that pie is drawn as a circle.
ax.set_aspect('equal')
plt.show()
Command:
$ python Downloads/pie_demo_features.py
Graphical output:
 |
| Figure 1 |
 |
| Figure 2 |
Python: Matplotlib: Path Example
Noteworthy:
matplotlib.path.Path
Path.MOVETO
Path.CURVE4
Path.LINETO
Path.CLOSEPOLY
matplotlib.patches.PathPatch()
ax.add_patch()
zip()
path.vertices
ax.grid()
ax.axis()
Command:
$ cat Downloads/path_patch_demo.py
Result:
"""
Demo of a PathPatch object.
"""
import matplotlib.path as mpath
import matplotlib.patches as mpatches
import matplotlib.pyplot as plt
plt.style.use('dark_background')
fig, ax = plt.subplots()
Path = mpath.Path
path_data = [
(Path.MOVETO, (1.58, -2.57)),
(Path.CURVE4, (0.35, -1.1)),
(Path.CURVE4, (-1.75, 2.0)),
(Path.CURVE4, (0.375, 2.0)),
(Path.LINETO, (0.85, 1.15)),
(Path.CURVE4, (2.2, 3.2)),
(Path.CURVE4, (3, 0.05)),
(Path.CURVE4, (2.0, -0.5)),
(Path.CLOSEPOLY, (1.58, -2.57)),
]
codes, verts = zip(*path_data)
path = mpath.Path(verts, codes)
patch = mpatches.PathPatch(path, facecolor='r', alpha=0.5)
ax.add_patch(patch)
# plot control points and connecting lines
x, y = zip(*path.vertices)
line, = ax.plot(x, y, 'go-')
ax.grid()
ax.axis('equal')
plt.show()
Command:
$ python Downloads/path_patch_demo.py
Graphical output:

matplotlib.path.Path
Path.MOVETO
Path.CURVE4
Path.LINETO
Path.CLOSEPOLY
matplotlib.patches.PathPatch()
ax.add_patch()
zip()
path.vertices
ax.grid()
ax.axis()
Command:
$ cat Downloads/path_patch_demo.py
Result:
"""
Demo of a PathPatch object.
"""
import matplotlib.path as mpath
import matplotlib.patches as mpatches
import matplotlib.pyplot as plt
plt.style.use('dark_background')
fig, ax = plt.subplots()
Path = mpath.Path
path_data = [
(Path.MOVETO, (1.58, -2.57)),
(Path.CURVE4, (0.35, -1.1)),
(Path.CURVE4, (-1.75, 2.0)),
(Path.CURVE4, (0.375, 2.0)),
(Path.LINETO, (0.85, 1.15)),
(Path.CURVE4, (2.2, 3.2)),
(Path.CURVE4, (3, 0.05)),
(Path.CURVE4, (2.0, -0.5)),
(Path.CLOSEPOLY, (1.58, -2.57)),
]
codes, verts = zip(*path_data)
path = mpath.Path(verts, codes)
patch = mpatches.PathPatch(path, facecolor='r', alpha=0.5)
ax.add_patch(patch)
# plot control points and connecting lines
x, y = zip(*path.vertices)
line, = ax.plot(x, y, 'go-')
ax.grid()
ax.axis('equal')
plt.show()
Command:
$ python Downloads/path_patch_demo.py
Graphical output:

Wednesday, September 28, 2016
Python: Matplotlib: Streamplot (2D Vector Field) Example
Noteworthy:
numpy.mgrid
numpy.sqrt
matplotlib.pyplot.subplots()
matplotlib.pyplot.cm.autumn
streamplot()
strm.linesspeed.max()
Command:
$ cat Downloads/streamplot_demo_features.py
Result:
"""
Demo of the `streamplot` function.
A streamplot, or streamline plot, is used to display 2D vector fields. This
example shows a few features of the stream plot function:
* Varying the color along a streamline.
* Varying the density of streamlines.
* Varying the line width along a stream line.
"""
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('dark_background')
Y, X = np.mgrid[-3:3:100j, -3:3:100j]
U = -1 - X**2 + Y
V = 1 + X - Y**2
speed = np.sqrt(U*U + V*V)
fig0, ax0 = plt.subplots()
strm = ax0.streamplot(X, Y, U, V, color=U, linewidth=2, cmap=plt.cm.autumn)
fig0.colorbar(strm.lines)
fig1, (ax1, ax2) = plt.subplots(ncols=2)
ax1.streamplot(X, Y, U, V, density=[0.5, 1])
lw = 5*speed / speed.max()
ax2.streamplot(X, Y, U, V, density=0.6, color='k', linewidth=lw)
plt.show()
Command:
$ python Downloads/streamplot_demo_features.py
Graphical output:
numpy.mgrid
numpy.sqrt
matplotlib.pyplot.subplots()
matplotlib.pyplot.cm.autumn
streamplot()
strm.linesspeed.max()
Command:
$ cat Downloads/streamplot_demo_features.py
Result:
"""
Demo of the `streamplot` function.
A streamplot, or streamline plot, is used to display 2D vector fields. This
example shows a few features of the stream plot function:
* Varying the color along a streamline.
* Varying the density of streamlines.
* Varying the line width along a stream line.
"""
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('dark_background')
Y, X = np.mgrid[-3:3:100j, -3:3:100j]
U = -1 - X**2 + Y
V = 1 + X - Y**2
speed = np.sqrt(U*U + V*V)
fig0, ax0 = plt.subplots()
strm = ax0.streamplot(X, Y, U, V, color=U, linewidth=2, cmap=plt.cm.autumn)
fig0.colorbar(strm.lines)
fig1, (ax1, ax2) = plt.subplots(ncols=2)
ax1.streamplot(X, Y, U, V, density=[0.5, 1])
lw = 5*speed / speed.max()
ax2.streamplot(X, Y, U, V, density=0.6, color='k', linewidth=lw)
plt.show()
Command:
$ python Downloads/streamplot_demo_features.py
Graphical output:
 |
| fig0 |
 |
| fig1 (w/ unknown error on right side) |
Subscribe to:
Comments (Atom)




